网络波动判定准则
网络波动一般都会体现在丢包率上,所以以丢包率差(简单方法)大于一定阈值则认为发生了网络波动。
丢包率 -最小丢包率 > 阀值
简单方法
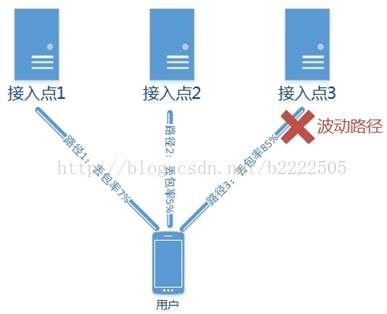
判断波动步骤:
- 找到所有路径中最小丢包率的路径:路径2;
- 将所有路径与这个最小丢包率路径相减得到差值;
- 如果差值大于阀值5%则认为有波动,可以看到路径3发生了波动。
判定为波动路径的样本量要大于阀值,对于那些样本量小于阀值的路径,即使发生波动了,也不会判定为波动,这样做的好处是处理简单,但这带来了一个问题:凌晨一般会导致样本量小于阀值,但运营商的割接和调整大部分在凌晨实施,对用户的影响不可忽略不计。
置信区间方法
(1) 丢包率15%,正常5%,样本量10000,可以认为波动了,因为比正常高出10%。
(2) 丢包率15%,正常5%,样本量20(丢了3个包),不能判定波动了,因为样本太少,碰巧丢3个包的可能性也不小的。
(3) 丢包率95%,正常5%,样本量20(丢了19个包),需要判定为波动,19个包都丢的可能太小了。
实际上这里隐藏了一个数学原理,可以简单描述为:假设40个样本带来的误差为30%(已经很大了,表明了可信度是很高的),那么实际丢包率可以简单描述为65%±30%,即丢包率在35% -95%之间,也就是说丢包率至少也有35%,而这个值远大于我们的阀值5%(这里为了描述的简单,实际上是丢包率差和5%相比),所以我们应该认为是波动。
上述区间在统计学中称为置信区间,所以判断网络是否波动的合理做法是判断置信区间的下限。
对于单个样本,要么丢包,要么不丢包,真实丢包率为p,那么丢包的概率就是p,这样n个样本可以看成n次伯努利试验,丢包率就是二项分布比例的估计。
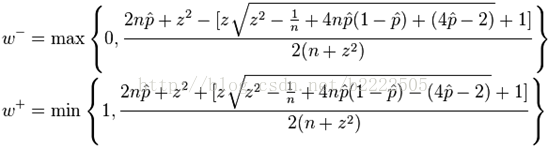
[w-, w+]就是置信区间,式中,n表示样本量,p^表示丢包率的极大似然估计,就是丢包数/样本量,z是统计学里的置信因子(我们取业界常用的95%置信度对应的z值1.960)。
按上述公式计算是单个丢包率的置信区间,而我们需要的是丢包率差的置信区间,即两个二项分布比例的差(详情看论文)
其他优化
其实我们可以直接把网络波动干预的粒度提升到1分钟级别,能感知波动就做干预,如果1分钟级别感知不到,则使用10分钟粒度累计数据,再不行就到1小时粒度,这种分级思想可以将波动感知的实时性做到最大化。
参考文献
- 置信区间(文中“赞成票比率”可类比为“丢包率”)
- http://www.ruanyifeng.com/blog/2012/03/ranking_algorithm_wilson_score_interval.html
- Newcombe,Robert G. Interval Estimation for the Difference Between IndependentProportions: Comparison of Eleven Methods. Statistics in Medicine, 17, 873-890(1998)
如果文章对您有帮助,欢迎扫描下方二维码赞助(一分也是爱噢),谢谢

